$+z$方向を向いた長さ$\Delta l$、電流$I$の微小ダイポールによる電界は、 アンテナから距離$d$のところにおいて \begin{align} \boldsymbol{E} &= \frac{k_0^2 Z_0 I \Delta l e^{-jk_0 d}}{4\pi} \biggl\{ 2 \cos\theta \left ( - \frac 1{\zeta^2} + \frac 1{\zeta^3} \right ) \hat{\boldsymbol{r}} + \sin\theta \left ( \frac 1\zeta - \frac 1{\zeta^2} + \frac 1{\zeta^3} \right ) \hat{\boldsymbol{\theta}} \biggr\} \\ &= j \frac{Z_0 I \Delta l e^{-jk_0 d}}{2 \lambda_0 d} \biggl\{ 2 \cos\theta \left ( -j \frac 1{k_0d} - \frac 1{(k_0d)^2} \right ) \hat{\boldsymbol{r}} + \sin\theta \left ( 1 - j \frac 1{k_0d} - \frac 1{(k_0d)^2} \right ) \hat{\boldsymbol{\theta}} \biggr\} \end{align} と書けます。ここで、$k_0, Z_0$は真空中の波数と波動インピーダンス、 $\zeta = -j k_0 d$、$k_0 = \dfrac{2\pi}{\lambda_0}$です。
$\zeta^{-1}$の項を放射界、 $\zeta^{-2}$の項を誘導界、$\zeta^{-3}$の項を静電界と呼びます。
これをプロットすると下図のようになります。 時間変動する場をアニメーションで表しています。
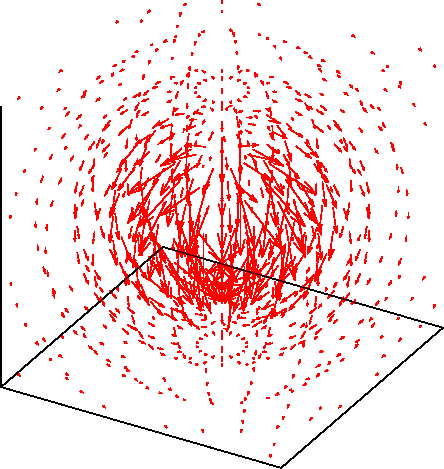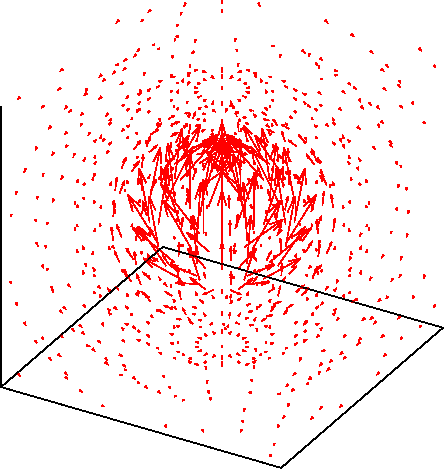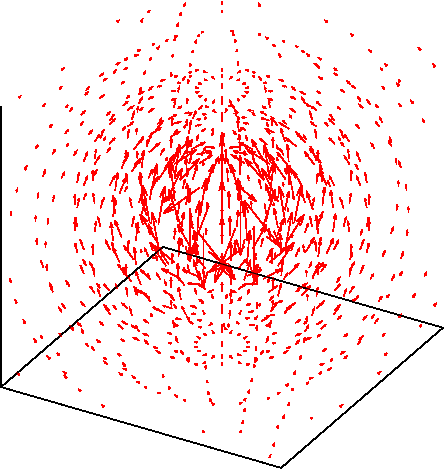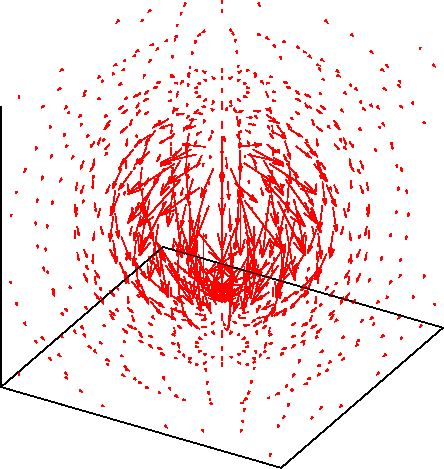
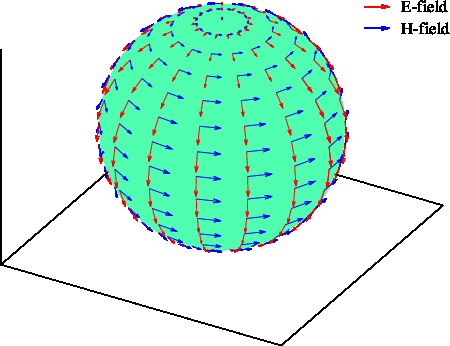
すこし見ずらいので、時間を止めて$d$が一定の面のみ表示すると 下図のようになります。 $kd = 1$の面ですが、ほとんど放射界のみです。 また、ここでは磁界(青)もプロットしています。 緑の球面は見易さのために付けています。 電界はほぼ$\theta$成分のみ、磁界は$\phi$成分のみになります。 また、$\boldsymbol{E} \times \boldsymbol{H}$は$+r$方向を向くことが 分かります。
指向性 アンテナは方向によって異なる電力の電磁波を放射します。 これを「指向性」と呼びます。アンテナの特性として指向性を表現するには 特殊な方法を用います。
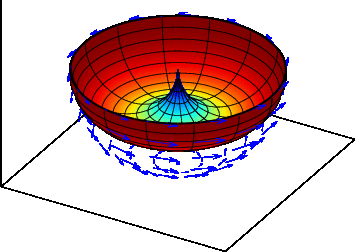
上の電界$\boldsymbol{E}$は$\theta$方向成分のみ持ち、 その大きさは$\sin\theta$に比例しています。 そこで、方向と電界の強さを表現する方法として、 中心からの距離を$R(\theta, \phi) = \sin\theta$とした曲面で指向性を表現します。 下図のようになります。
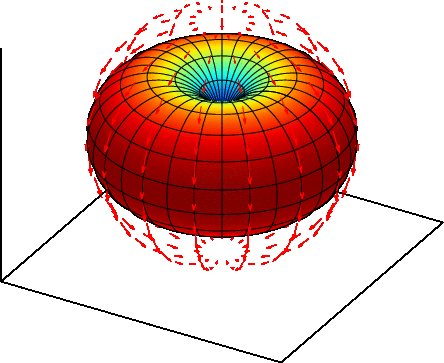
E面 3次元曲面を描いた場合は、全体像は理解しやすいですが、細かな値が 分かりません。そこで、実際には3次元曲面の断面で表示します。 「電界ベクトルに平行な面」の断面をE面と呼びます。
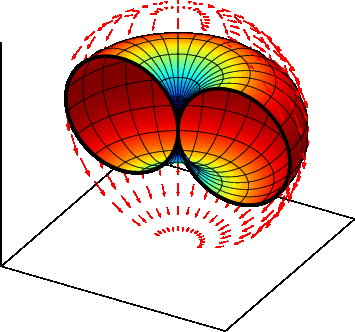 |
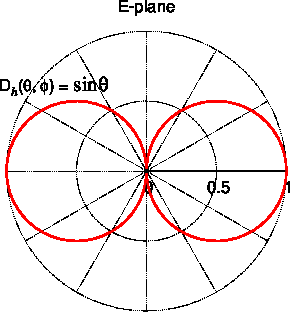 |
|
| 曲面を切って断面にしたもの | E面の指向性 |
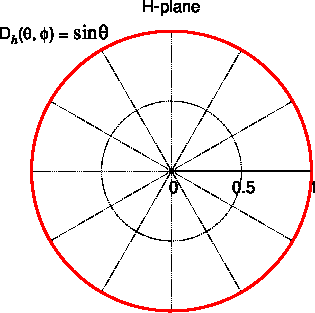
H面 同様に磁界に平行な面の断面をH面と呼びます。
 |
 |
|
| 曲面を切って断面にしたもの | H面の指向性 |
通常は3次元の曲面は示されず、E面とH面のみが示されます。 E面、H面の図から指向性を想像できるようにして下さい。
微小ダイポール・アンテナと半波長ダイポール・アンテナの指向性 微小ダイポール・アンテナの指向性関数 $D_h(\theta, \phi) = \sin\theta$、 および半波長ダイポール・アンテナの指向性関数 $D_{\lambda/2}(\theta, \phi) = \dfrac{\cos(\frac{\pi}2 \cos\theta)}{\sin\theta}$ をプロットした図(E面)を下に示します。
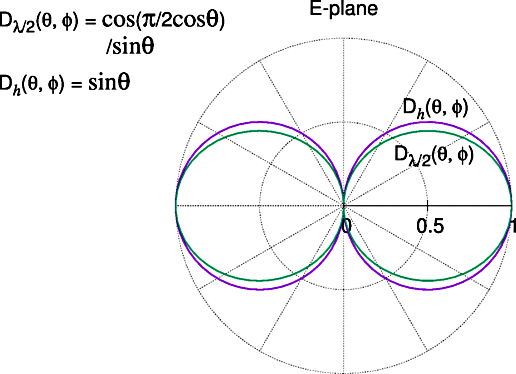
$D_{\lambda/2}(\theta, \phi)$の方が指向性がやや細く、 放射された電力は$\theta = \dfrac{\pi}2$の方向により強く集中している ことが分かります。